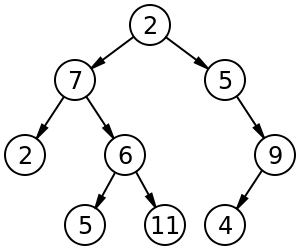
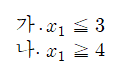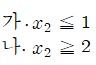비선형계획법은 목적함수나 제약조건을 선형으로 나타낼 수 없는 것을 말합니다.

선형계획법에선 심플렉스라는 강력한 방법을 이용해서 풀었습니다 그리고 정수계획법에서는 단체법은 쓸 수 없었으나 제약 완화를 통해서 다시 선형계획법으로 만들어 심플렉스를 적용하거나 특수한 기법을 통해 심플렉스를 적용하여 빠르게 정수해를 구할 수 있었죠.

그러나 비선형계획법에서는 이 좋은 심플렉스를 사용하지 못합니다.

예를들어 초밥먹은 갯수에 따라서 만족도가 위와 같다고 합시다

그러면 저 그래프가 최대화가 될 때 돈도 아끼고 만족도도 챙기고 일석이조겠죠??

비용은 한정되어 있는데 얼마나 초밥을 먹어야할까요?

여러가지 제약조건이 걸려 있는 상황에서는 저런 간단한 곡선조차 문제를 매우 풀지 못하게 만듭니다.

선형계획법에서는 제약조건이 많이 걸려있어도 연산 난이도만 올라가지 문제를 못 건드리는 수준까지는 아니였거든요

다른 예로 양에 따른 가격의 감소 문제도 비선형입니다.

(위 그래프 공유합니다 : www.geogebra.org/calculator/ftw7kytb)

만약 선박에 싣은 물건의 총량에 따라 운송비가 할인되면(규모의 경제) 싣는 량에 비래해서 총 비용은 위 그래프와 같습니다. 여기서는 싣는 량에 따라 3단계로 구분하였습니다.

1단계는 싣는량에 비례해서 5원

2단계는 싣는량에 비례해서 2원

3단계는 싣는량에 비례해서 0.5원

이것을 어떻게 풀면 최적으로 선박에 싣을 수 있는 량이나 비용을 구할 수 있을까요?

위의 그래프 개형을 보면 쉽게 예측은 가능하지만 이 또한 여러 제약조건이 덕지덕지 붙기 시작하면 답이 없어집니다.

예를 들어볼까요?

5개의 품목이 있는데 각각의 무게와 이득은 다음과 같습니다.

A = 10      2

B = 20      2.1

C = 25     1.8

D = 30     4

E = 35      3

(단위 Kg)

이것을 선박에 싣는다고 할 때 총 용량은 50Ton 까지 싣을 수 있으면 각각의 물건을 몇개 싣는게 가장 이득이 클까요?

목적은 이득을 가장 최대화하는 것.. 그러면 목적함수는 이렇게 나타낼 수 있겠네요

MAX : 2A+2.1B+1.8C+4D+3E - 운반비용 함수(A+B+C+D+E)

s.t.   : 10A+20B+25C+ 30D + 35E <=50000

흠 선형계획법으로 어떻게 풀지 감이 안잡히네요

그러면 한가지 생각을 해봅시다. 예로부터 복잡한 문제들의 해법을 구하기 위해서 먼저 시행해왔던 기본적인 규칙이 있습니다.

바로 규칙없이 그냥 심플하게 단순한것부터 보는 것입니다.

비선형계획법의 가장 단순한 영역은 목적함수만 생각할 때이며 이것을 제약조건이 없는 최적화라고 합니다.

위에서 다시 한계효용 곡선을 가져왔습니다.

목적함수만 두고 볼때 가장 이득을 볼 수 있는 지점은 명확합니다.

바로 그래프가 오목하게 올라와 있는 부분이죠

이처럼 볼록하거나 오목한 함수는 최대값과 최소값을 찾기가 쉽습니다

정확히는 지역 최소값이나 지역 최대값이 전역 최소값과 전역 최대값입니다.

아하 그러면 오목하거나 볼록한 함수는 공략할만하다는 것을 알았습니다.

이러한 것을 볼록 집합(혹은 오목 집합)이라고 합니다.

그런데 이런 말이 나올 수가 있습니다. "볼록집합만 가지고 뭘할 수 있겠어?? 그냥 진짜 특수한 경우만 쓸 수 있는게 아니야??"라고요

맞는 말이긴 합니다만 아래 예제를 봅시다

y=x는 실수 전체에서 오목집합입니다

이 y=sinx 그래프는 오목집합이 아닙니다.

그런데 정의역을 0~PI(3.14)까지로 줄이면

이 함수는 오목집합이 됩니다.

거기다 0~PI/2까지로 정의역을 줄여도 오목함수가 됩니다.

이제 이해가 되나요??

원래 목적함수가 오목집합이 아니더라도 제약조건에 의하여 오목집합이 될 수 있고 또 그게 아니라면 몇가지 조건을 완화하거나 추가함으로 오목집합으로 만들면되기 때문에 중요한 것입니다.

거기다 지금은 제약조건은 고려 안한다고 했죠?

위에서 설명을 명제으로 쓰면 다음과 같습니다.

먼저 지역 최대값을 만족하는 조건을 정의하면

그리고 지역 최대값이 전역 최대값으로 갈 수 있는 조건을 따져봅시다.

여기서 엄격한 오목함수라는 말이 나왔는데 자세한것은 책을 보시는게 좋고 일단 그냥 y=x는 엄격한 오목함수가 아니고 그냥 오목함수라는 것입니다.

이제 이 오목함수라는 개념을 적용해서 해를 구할 수 있습니다.

어떻게 구하냐고요?

생각해봅시다 오목집합의 경우는 위 조건에 의해서 몇가지 사실과 미적분학에서 기초지식 그리고 저희가 알고 있는 몇가지 상식만 가지고 있으면 어떻게 구하는지 이해가 가능합니다.

사실1 - 함수 F(x)의 경우 오목집합이면 지역 최대값이 전역최대값을 만족한다

사실2 - F(x)의 경우 미분한 그래프에서는 양의 기울기를 가지다 최대값에서 0을 찍고 음의 기울기를 가진다.

사실3 - 오목집합 혹은 볼록집합인 경우는 해가 양수가 나오는 구간과 음수가 나오는 구간이 있다.

사실4 - 중간값 정리에 의하여 양수가 나오는 구간과 음수가 나오는 구간 사이에 F'(x)의 해가 존재한다!!!

      -> 따라서 이 구간을 잘 살펴서 좁히면 F'(x)의 해 지점인 c를 찾을 수 있고 결국 최적화를 만족하는 곳은 c라는 것을 알 수 있습니다. 

이 방법을 바로 이분법(bisection method)라고 합니다.

위키피디아에서 사진을 퍼왔습니다.

이렇게 보면 함수 F(x)가 0이 되는 지점을 찾기 위해서 구간을 정해두고 계속 계산을 하여 중간값 정리를 응용하여

F(b)<0를 만족하는 것을 확인하고 있습니다.

물론 완전한 해를 보장하지는 못하지만 어느정도 구간은 추정할 수 있죠 마치 통계학에서 말하는 구간추청처럼 말이죠

이제 예제를 보면서 하는 방법을 알아봅시다.

일단 몇가지 정의를 해야할 변수가 있습니다.

마지막에 저만의 언어를 넣었습니다. 일일히 수식 입력하기 귀찮아서 제가 "x바"라고 하면 위에서 본 표현을 떠올려주시면 되겠습니다.

그러면 절차를 간단하게 소개를 해보면 오목집합인 경우

그러면 가장 먼저 해야될 일은 과연 위의 1.일까요?

흠.. 가장 먼저 해야될 일은 오목함수라는 것을 보이는 거겠죠?

이계도함수를 구해보면 -12(3x^2 + 5x^4) 가 되는군요

x가 실수 어떤 값을 넣어도 저 함수는 항상 음수값를 가지고 x에 0을 넣으면 함수 값은 0이 되니 오목함수라고 할 수 있습니다.

그 다음 대강 지점을 구해보죠

일단 원래 함수의 한 번 미분한 함수

12(1-x^3 -x^5)에서 x에다 간단하게 0을 넣어봅시다

그러면 -12가 나오네요

그리고  1을 넣으면 음수 나올거같은데...

-12정도 나오네요

그러면 0과 1 사이에 중간값정리의 의하여 해가 존재하는 건 확실합니다.

다음 0과 1 사이값인 0.5를 생각해봅시다.

0.5에서 기울기 값은 10.125가 나옵니다.

이 값은 0 이상의 양수이기 때문에 다시 이것을 x 언더로 둡시다.

그리고 또 사이의 값인 0.75를 구하고

다시 구해보면 4.0xxxx 정도가 나오고 다시 x 언더에 넣고 ... 무한 반복합니다. 원하는 만큼의 정밀도가 나올때까지.......

표로 표현하면 다음과 같습니다.

그러면 이제 어떻게 비선형에서 오목 또는 볼록집합일 경우 푸는 방법은 알았습니다.

하지만 아직 못한 이야기도 있습니다. 바로 변수가 여러개일 경우와 (x1, x2 ... ) 제약조건이 걸려있는 경우에 관한 것이죠

비선형계획법이 상당히 난해하다보니 너무 길어지네요 다른 포스트에서 이 다른 경우에 관해 다루겠습니다.

일반화된 분지절단법이란 어떠한 정수계획법에도 쓸 수 있는 분지절단법을 말합니다.

저번에 썼던 포스트에서 정수계획법에 대한 간단한 설명과 기초 개념을 다뤘습니다.

그 후 정수계획법을 푸는 방법 중 하나인 분지절단법에 대해서 알아봤고 배낭문제에 적용하여 풀이를 해봤습니다.

그런데 생각해봅시다 저번에 풀었던 배낭문제는 결국 하냐 안하냐로 귀결되는 정수계획법의 한 분야인 0-1계획법 문제였습니다. 그러면 다른 정수계획법 문제에 분지절단법을 적용하려고 하면 어떻게 될까요??

저번에 다뤘던 배낭문제를 다시 꺼내봅시다.

여기서 분지절단법으로 풀때 X1을 분할 변수로 두고 0일 때와 1일 때로 두고 풀었습니다. 

이렇게 말이죠

그리고 쭉쭉 분할해서 다음과 같은 그림을 얻었습니다.

그러면 만약 문제가 0-1계획법 문제가 아니라 그냥 정수계획법문제면 처음 시작할 때 어떻게 분할할지도 막막합니다.

그래서 이번 포스트에서는 다른 정수형문제도 막힘없이 풀기 위해서 일반화된 분지절단법을 알아보도록 합시다.

기본적인 초반의 흐름은 0-1계획법에서 했던 내용과 같습니다.

처음엔 하한을 무한으로 둔다... 상한은 문제를 단체법으로 푼 뒤 나오는 값을 사용한다. 이렇게 말이죠

근대 분지에서 약간 틀립니다.

한번 보시죠 내용은 (박순달 저)경영과학 제 3판 민영사에서 가져왔습니다.

단계 2. 분지

(1) 최적해에서 정수가 아닌 변수를 선택한다.

(2) 원문제에 다음 제약식을 각각 추가한 두 개의 새로운 문제를 문제목록에 등록한다.

단계 3  탐색

문제목록에서 문제 하나를 선택한다. 만일 비어 있으면 끝난다.

여기서 분지를 잘봅시다. 저기서 원문제에 관해 제약식을 추가하여 두 개의 새로운 문제를 등록하는 과정은 0-1계획법 분지계획법 풀이에서 보았던 트리가 생성되는 과정입니다.

또한 일반화된 분지절단법의 경우 저 제약식을 원래 문제에 집어 넣어 풀이를 하게 됩니다.

그런데 잘생각해봅시다.

0-1계획법에서는 처음에 x1에 0과 1을 넣어 분지했죠?? 이렇게 말이에요

그런데 잘생각해보면 이것 또한 제약식을 추가한 것과 같습니다. 

그 다음 저 제약식을 포함한 두개의 자식 노드로 나뉜거죠

아하 그럼 이제 눈에 보입니다.

바로 본질적으로 0-1계획법 풀이와 달라지지 않았다는 것이죠

전혀 새로운게 아니라 제약식에 부등호가 추가되었을 뿐입니다.

이제 어떻게 돌아가는지 대충 보이시죠?

그러면 문제 하나 풀어봅시다.

먼저 단체법으로 위 식을 풀어보면 

x1=13/4 , x2= 5/4 , x3=0, x4=0 그리고 최대값은 75/4입니다.

따라서 상한을 75/4=18.xxx로 설정할 수 있겠군요

그럼 먼저 간단하게 x1에 대해서 분지하도록 하고 기준을 3에 둡시다. 

일단 기준을 정했으면 제약식은 다음과 같습니다.

그 다음은?? 그냥 x1에 위 수식을 각각 대입하면됩니다

그러면 먼저 왼쪽 노드부터 생각해봅시다 

왼쪽 노드를 풀기 귀찮으니 단체법 계산기에 넣으면...

x1=3

x2=1.5

x3=0

x4=0.5    그리고 z값은 18이 되는군요

일단 이 해는 정수해가 아니므로 한번 더 분지시켜봅시다

왼쪽 자식노드를 x2에 대해서 기준값 1( 1은 0과 1 즉 2개를 내포하고 있죠?)에 관해서 분지하면

다음 왼쪽 노드를 계산기 넣고 돌려보면

x1=3

x2=1

x3=1

x4=1

Z=17 이 나옵니다

드디어 찾고 찾던 정수해 단! 하나가 나왔군요

일단 그러면 저 정수해를 기록해두고 하한을 17로 둡시다

다음 오른쪽도 돌려봐야죠?

오른쪽같은 경우는

x1=2.5

x2=2

x3=0

x4=1.5

z=16.5가 나옵니다

그런데 z값이 왼쪽에서 나온 하한인 17보다 작군요

그러면 더 이상 오른쪽 노드는 분지할 필요가 없습니다.

다음으로 다시 부모 노드로 돌아가서

이번엔 오른쪽 노드를 파해쳐봅시다

오른쪽노드의 해는 비가해 즉, 해를 구할 수 없다고 나옵니다.

그러면 현재까지 구한 정수해는 한개밖에 없죠??

그러면 이 문제의 해답은 

x1=3

x2=1

x3=1

x4=1 이며 Z=17 이 나옵니다

정리

이렇게 일반화된 분지한계법의 풀이는 살짝 더 복잡하지만 익숙해지면 정수계획은 문제없이 풀 수 있는 강력한 도구 중 하나입니다.

일반적으로 동적계획 문제는 최적 경로 찾기나 지정된 3곳 중에 금액이나 사람 등을 몇 개 투입해야 최대 이익이 될 수 있는지 등을 계산하였습니다.

그런데 만약 다음과 같은 경로 찾기 문제를 생각해봅시다

A   --   B    --   D

    ㄴ  C   ┘     

여기서 A에서 B와 C로 갈 수 있다고 할 때 그냥 거리가 짧은 쪽을 고르면 쉽게 풀리는 문제입니다.

그런데 만약 A에서 B와 C를 확률적으로 갈 수 있다고할 때  즉, 두 길이 50%와 50%확률로 갈 수 있다고 할 때 는 어떻게 될까요?

가장 기본적인 생각은 기댓값이라는 아이디어입니다.

로또복권 한장을 사면 기댓값이 22원 정도... 만원내기로 동전 던지기를 할 때 기댓값은 5천원...

이렇게 실제 실현된 값은 아니지만 기댓값이라는 개념으로 위의 문제에서 확률에 따른 길의 길이를 기댓값으로 수치화 할 수 있습니다. 따라서 이 기댓값을 가지고 동적계획법 계산이 가능해집니다.

예를 들어보죠

여러분은 아주 잘나가는 햄버거 요리사입니다.

 그런데 어느날 아주 유명한 미식가가 찾아와 햄버거 하나를 주문합니다.

이 미식가를 만족시키면 자신의 평판이 오를것이 분명하기 때문에 최대한 열심히 만들려고합니다.

그런데 미식가가 어떤 취향인지를 몰라서 일단 햄버거를 여러개 만들 생각도 해봅니다.

과연 이 미식가를 만족시킬 수 있을까요??

이때 확률론적 동적계획법을 사용하면 미식가를 최대한으로 만족하고 여러분의 평판과 임금이 오를 수 있습니다!! 

일단 저기서 추가적인 조건이 있습니다.

  1. 일단 여러분은 한번 요리를 시작하면 무조건 3천원이 소모되며 햄버거 하나당 추가적으로 1천원이 더 소모됩니다.

  2. 한번 요리를 시작하면 5분이 소요됩니다.

  3. 임의로 만든 햄버거 하나가 미식가를 만족시킬 확률은 50%이며 모든 햄버거가 입맛에 안맞으면 1.6만원의 손해를 입습니다.

  4. 미식가는 15분동안 기다려 줄 수 있습니다.

이때 어떻게하면 최소한의 소모로 미식가를 만족시킬 수 있을까요?

그러면 잘 생각해봅시다. 3개를 만들었는데 미식가가 만족하는 퀄리티의 햄버거가 2개라고한다면 의미가 있을까요?

미식가는 하나의 햄버거만 주문했기 때문에 1개 이상을 만족시키는 것은 의미가 없습니다.

그러면  목표는 최소한으로 만들어서 최대한 미식가를 만족시킬 수 있는 L값을 정하는 것입니다.

따라서 미식가가 만족할 확률은 다음과 같이 정해집니다.

이제 햄버거에 대한 기댓값을 정의해봤으니 동적계획법에서 중요한 3가지 요소 단계, 상태, 결정변수를 정의해 봅시다.

먼저 단계!

여기서는 단계란 미식가가 최대 15분을 기다려줄 수 있고 요리 한번하는데 5분이 소요되므로 총 3번 요리할 동안 기다려 줄 수 있습니다. 

따라서 단계는 3개가 있다고 볼 수 있습니다.

그러면 상태와 결정변수를 분석해봅시다.

결정변수는 뭘까요? 여기서 변경할 수 있는 숫자는 한번에 생산하는 햄버거의 갯수뿐이죠?

마지막으로 상태는 특정 단계에서 만족 했는가 안했는가 입니다.

그래야 만족하는 루트로 갈지 만족하지 못하는 루트로 갈지 정할 수 있거든요

그러면 이제 식을 정의해봅시다

한 단계당 무조건 요리를 해야하고 햄버거 수에 따라 비용이 달라지므로 다음과 같이 나타낼 수 있습니다.

3+Li

따라서 이 문제의 동적계획법 수식은 다음과 같습니다.

따라서 이것을 다시 동적계획법에서 풀듯이 뒤에서 부터 풀면 다음과 같습니다.

어때요 그냥 동적계획법과 다를바없이 쉽지 않나요?

운용과학(OR)에서 여러 모형들의 기원은 그렇게 뚜렷하지 않습니다. 선형계획법이나 정수계획법 수송문제 등등...

그런데 이 동적계획법은 창조자가 잘 알려져있습니다 바로 리처드 벨만이라는 사람으로 동적계획법이 다이나믹 프로그래밍이 된것도 이 사람이 다이나믹이라는 말이 멋있어서 붙였기 때문이라는 설이 있습니다.

따라서 다이나믹이라는 뜻도 동적이라는 뜻도 이 계획법과는 상관이 없는 뜻입니다.....

여하튼 이번 포스트에서는 동적계획법이 무엇이며 어떻게 쓰이는지 알아봅시다.

동적계획법은 최적의 해를 찾기 위해 이전에 구한 답을 이용하여 문제를 푸는 기술 혹은 방법을 말합니다.

이렇게 써두면 직관적으로 이해가 안갑니다

재미있는 예를 들어보죠

옛날 어느 중동의 나라에 한 청년이 살고 있었습니다. 청년은 골동품을 모으는 취미가 있었는데 어느날 골동품 시장에서 신비한 램프를 샀습니다. 그리고 램프를 보관하기 위해서 닦는 순간 램프의 요정이 나타난것입니다!

램프의 요정은 램프의 봉인을 풀어준 대가로 보물을 준다고 합니다.  요정은 세계에서 가장 진귀하다는 보물 1위부터 100위까지를 가지고 있는데 전부는 줄 수 없고 자신이랑 게임을 해서 한개만 받을 수 있다고 합니다.

게임은 요정이 보물 100개를 30초마다 하나씩 보여주는데 자신이 원하는 보물에서 멈춰! 라고 말하면 그 보물을 준다고 합니다. 다만 이미 지나간 보물은 받을 수 없고 당연히 앞으로 나올 보물 또한 받을 수 없습니다.

청년은 보물을 보자마자 요정이 지금까지 보여준 보물들의 상대적인 순위를 제대로 파악할 수 있다고 할 때 과연 보물을 몇번째 보여줄 때 쯤 멈추는게 현명할까요?? 

이 문제는 동적계획법 문제입니다. 최적의 해는 언제쯤 멈춰야 최대의 가치가 되는지 그리고 보물의 상대적인 순위를 파악할 수 있으므로 이전 구한 답을 이용해서 문제를 풀게 됩니다. 동적계획법의 정의에 딱 맞는 문제입니다.

참고로 위 문제의 정답은 약 33번째 쯤에 보물을 받는게 가장 가치가 높습니다.

이렇게 복잡한 문제도 풀 수 있는 동적계획법! 그런데 아직까지는 좀 아리송합니다. 특히 지금까지 선형계획법으로 잘 풀어왔는데 동적계획법이 무슨 소용이냐!라는 말이 있을 수 있습니다. 그래서 어떤 문제를 동적 계획법으로 풀 수 있는지 알아봅시다.

먼저 중요한 개념은 최적성의 원칙(principle of optimality)가 없으면 동적계획법으로 풀 수 없습니다!

그러면 최적성의 원칙이 무엇인지 알아야겠죠?

예를 들어 봅시다

여러분은 의사입니다. 근대 이웃마을에 위급한 환자가 있다고 연락이 와 급하게 가야합니다. 

이웃마을까지 가는데 다음과 같은 루트가 있다고 할 때 어떤 루트로 가야할까요?

이런 최단경로를 찾는 문제는 대표적인 동적계획법 문제입니다.

그런데 모든 최단경로 문제가 동적계획법으로 풀 수 있을까요?

만약 위 루트에서 A루트로 가면 길이 너무 험해서 포인트에서 환자까지 가는데 1시간이 걸립니다.

편한 길인 B루트로 가면 포인트에서 환자까지 가는데 30분이 걸립니다.

이렇게 같은 지점을 가는데 그 지점에서 다음 지점으로 이동할 때 걸리는 시간이 이전 루트에 영향을 받습니다.

이렇게 되면 최적성의 원칙이 깨졌다고 합니다.

그러면 이렇게 최적성의 원칙이 깨지면 왜 동적계획법으로 풀 수 없을까요?

핵심은 이전 답을 재활용한다는 것에 있습니다.

만약 이전 루트에 따라서 포인트에서 환자까지 가는 길에 영향을 준다면 의사 위치에서 포인트까지 가는 길이 짧은 루트는 아무 상관이 없습니다.

짧은 루트로 갔는데 오히려 포인트에서 환자까지 가는데 시간이 다른 루트에서 온 것보다 더 걸릴 수도 있는 것이지요

기본적으로 최단경로를 찾는 문제는 A 지점에서 (정확히는 단계 안의 노드 입니다만 단계라는 용어는 나중에 다시 설명하겠습니다.)  B 지점까지의 최단경로를 알면 A지점에서 C지점으로 가는데는 B에서 C로 가는 최단 경로만 구하면됩니다.

그렇게 되면 앞서 미리 구한 A에서 B까지 가는 최단 경로 답을 이용하여 그냥 더하면 되죠 

min(AB) + min(BC) = min(AC) 

하지만 최적성의 원칙이 깨지면 위와 수식의 방식을 쓸 수 없습니다.

AB로 가는 최단 경로가 BC의 최단 경로에 영향을 주기 때문에 AC의 최단 경로라는 것을 보장하지 못하거든요

그러면 이제 어떤 문제가 동적계획법으로 풀 수 있는지를 알았으니 특정 문제를 동적계획법으로 나타내는 방법을 알아봅시다.

문제를 정의하기 위해서 동적계획법만의 세 가지 중요 변수가 있습니다.  

단계(Stage) : i 

: 동적 계획법의 단계를 나타냅니다.

상태(state)  : s

: 특정 단계에서 선택할 수 있는 노드를 말합니다

결정변수(control) : x 

: 특정 단계에서 다음 단계로 가는 최적의 상태를 선택하는 것을 말합니다.

이것을 수식으로 나타내면 다음과 같습니다.

이렇게 개념만 보면 머리가 아프니 정리할겸 예제를 봅시다.

삼송(三松)이라는 기업은 여러개의 자회사들을 두고 있는 초거대 기업이있다고 합시다.

이 기업에서 분석하길 자회사 3곳(삼송전자, 삼송자동차, 삼송중공업)에 경영비상이 걸려 특별경영개선팀을 파견하려고 합니다.

특별경영개선팀은 총 5개의 그룹이 있으며 각 회사마다 파견되는 개선팀에 따라 이득이 다음과 같다고 할 때 어떻게 경영개선팀을 보내는게 최대한 이득을 볼 수 있을까요?

 (단위 : 억원)

여기서 전자와 중공업은 최대 팀을 2개 자동차는 3개를 보낸다는 정책이 있습니다.

일단 이문제는 목표가 명확합니다. 최대한 돈을 벌자!

그리고 자원은 특별경영개선팀 5그룹이 있습니다.

동적계획법 풀이 1단계는 단계, 상태, 결정 변수를 정하는 것입니다.

먼저 이 문제에서 결정 변수를 정의해보면 [특정 그룹에 얼마나 많은 개선팀을 파견할 것인가??]가 됩니다.

그리고 단계를 나눠보면 

삼송전자-> 삼송자동차 -> 삼송중공업

이렇게 3단계로 나뉠 수 있습니다.

각 단계에서 변화하는 요소는 과연 무엇일까요?

이게 동적계획법의 킵 포인트로 바로 개선팀의 남는 개수가 변화합니다.

정확히는 자원이 변화할 수도 있는 가능성을 따지는 겁니다.

다시 각 단계에 상태를 부여해봅시다.

 S1              S2                 S3

삼송전자-> 삼송자동차 -> 삼송중공업

각 상태에서의 팀의 개수는 다음과 같습니다.

S1 = 5

S2 = 5-X2 = S1 - X2 

S3 = 5-X2-X3 = S2 - X3

그 다음으로 해야할 것은 각 단계에 관해서 재귀적 관계를 정립하는 것입니다.

요런 관계

저 위 수식은 동적계획법에서 매우 중요하므로 동적계획법을 요령껏 잘 쓸려면 외워둡시다

이제 저 수식으로 문제를 푸는데 푸는 방법이 다소 특이(?)합니다. 

이런 미로 찾기 아시나요??

미로 찾기는 출구에서 이리저리 복잡하게 헤매면서 푸는 재미가 있죠

근대 이 미로찾기를 쉽고 간단하게 풀 수 있는 방법이 있습니다.

바로 출구부터 시작하는 것이지요

그러면 놀랍게 입구에서 시작하는 것보다 더 빠르게 풀 수 있답니다.

그 이유는 미로찾기 알고리즘에 있습니다. 

(시간 나시면 한번 보시는걸 추천합니다 동적계획법으로 미로찾는 알고리즘입니다)

즉 출발 지점에서 부터 진행하지 않고 출구지점에서 부터 진행하자!! 이게 동적 알고리즘의 핵심입니다.

그러면 다시 삼송 기업의 회생(?) 팀 파견 문제로 돌아가봅시다

아까 본 재귀 수식에 i=3일 때를 넣습니다. 즉 마지막 단계에서 수식은 시작합니다.

그러면 4단계가 없으므로 자동적으로 3단계까지 누적이득과 3단계에서의 이득은 같게 됩니다

좀 더 식을 전개하면

이렇게 쓸 수 있습니다.

그러면 각 식마다 키포인트가 되는건 

이것을 구하는게 됩니다.

그러면 저 수식이 없는 단계는 몇단계였죠?? 그렇습니다 마지막 단계인 3단계가 없죠

그러면 3단계부터 상태에 따른 이득을 표로 나타내면 다음과 같습니다.

1단계에서 S1=5라고 위에서 언급했으므로 상태가 5일때만 계산해주면 됩니다

따라서 파견은

삼송전자, 삼송자동차, 삼송중공업 순서로

0개, 3개, 2개팀을 파견하던지

2개, 2개, 1개팀을 파견하는 것이 최적파견이 됩니다.

동적계획법은 문제에 따라서 약간의 변형이 필요할 수 있습니다 

다른 포스트에서 유명한 문제인 배낭 문제를 동적계획법으로 풀어보고 비교하면서 알아보면 동적계획법 풀이에 대한  좋은 시각을 가질 수 있습니다. 

정수계획법은 간단히 말하자면 선형계획법에서 정수해만을 인정하는 경우를 말합니다.

그래서 식은 선형계획법 식과 다름이 없습니다.

단지 제약이 해가 정수여야 한다는 것입니다.

그러면 이런걸 어디다 써먹을까요? 

바로 결정 문제에서 많이 쓰입니다. 서울에 집을 5채를 사겠다고 하지 4.3채를 사겠다고 하지 않잖아요

그런데 이러한 정수계획법에서 일부는 정수 해가 나오고 일부는 실수 해가 나올 수 있는데 이것을 혼합정수계획법(MIP)라고 합니다.

정수계획법에서는 이 정수라는 놈 때문에 선형계획법에서 편리하게 사용했던 단체법을 사용할 수가 없습니다.

그래서 정수계획법에서는 각 문제에 따라 알맞은 계산방법이나 근사해를 구하는 발견적 기법 즉, 휴라스틱을 사용합니다.

정수계획법 문제 예를 봅시다

많이들 들어본 배낭문제가 그 예중 하나입니다.

재미있게 보셨나요?

도둑은 결국 자전거만 끌고 집에 가는군요

영상에서는 욕심쟁이 알고리즘이 나왔지만 이거는 나중에 알아보도록 합시다.

이처럼 도둑도 포기하게 만든 배낭문제! 쉬워보이지만 깊게 파고들면 매우 복잡한 문제입니다.

예시를 들기 위해 위에서 나온 물품의 가치는 다음과 같다고 합시다.

가방에는 최대 20KG까지 들어갈 수 있으므로 위 문제를 수식으로 나타내면 다음과 같습니다.

여기서 X1이나 X2가 0.5와 같은 값을 가질 수 있을까요?

그러면 가장 가치있는 자전거를 0.5개.... 즉 반토막을 내서 가져가면 가치가 50만원일까요?

이렇게 가져가냐 안가져가냐를 따지는 문제... 더 포괄해서 하는가 않하는가를 따지는 문제를 0-1계획법이라고 합니다. 

그러면 정수계획법의 대략적인 문제의 형태가 보이기 시작합니다.

그러면 이제 이 문제를 해결할 수 있는 해법에 대해 토의하기 

이러한 정수계획법의 휴라스틱 해법으로는 두가지가 있습니다.

절단평면법

분지한계법

이 두가지 방법을 모두 설명하려고하면 분량이 매우 많기 때문에 절단평면법은 다른 포스터에서 다뤄보기로 하고 이 포스터에서는 분지한계법을 알아보도록 합시다.

그러면 차근차근 해법을 살펴보도록 합시다.

 *분지한계법(Branch-and-bound technique)

이 방법은 모든 가능해를 계산하는 열거식의 일종입니다.

모든 해를 계산하는게 바보같고 택틱컬하지 않다고요?

아뇨 모든 가능한 방법을 검토해보는건 100% 가장 확실한 방법입니다.

단지 시간이 조금 오래 걸릴뿐이죠..

분지한계법은 쪼개서 정복하는 알고리즘입니다. 큰 해영역에서 진짜 이 영역은 아무리 봐도 아니다싶은 부분은 잘라내고 남은 영역에서 탐색하고 또 잘라내고 탐색하는것을 반복하는거죠.

따라서 분지한계법은 이진트리의 형태를 띄고 있습니다.

대강 이런 느낌...

그리고 또 중요한건 탐색하면서 해의 상한과 하한을 정한다는 특이한 점이 있습니다.

이거는 지금 설명하면 이해가 잘안될 수 있으니 예를 보고 갑니다.

실제 알고리즘은 3단계로 간단한 편입니다. 

분지 -> 한계설정 -> 살펴보기 -> 분지 -> 한계설정 -> 살펴보기 .... 

위 배낭문제를 예로 들어봅시다.

먼저 위 식에서 수정해야할 점은 해가 정수라는 조건을 없애는 것입니다.

더 정확히는 해가 0~1까지로 제한합니다.

이렇게 해의 조건을 완화하는 것을 Relaxation이라 하는데 조건을 완화함으로 더 쉽게 문제를 풀 수 있습니다.

위 수식을 제약조건을 완화하여 다시쓰면 다음과 같습니다.

다음 해야할 것은 위 수식을 일단 단체법으로 풀어봐야합니다.

풀면 최적해는 (0, 1, 0, 0.4)로 나오며 값은 90이 되는데 이 90이라는 값이 바로 앞으로 풀면서 나올 모든 값들의 상한이 됩니다.

왜냐하면 정수해는 실수해보다 값이 반드시 같거나 작기 때문입니다.

비유를 하자면... 만약 자동차와 비행기가 같은 목적지로 간다고 생각해봅시다. 비행기는 밑에 건물이 있던 없던 쌩하고 목표까지 날아갈 수 있는데 자동차는 도로나 여러 신호를 봐가면서 가야하기 떄문에 훨씬 시간이 오래 걸립니다.

이때 공중을 아무 제약조건도 없는 상황 그리고 도로나 여러 신호상황을 정수 제약조건으로 봐도 무방합니다.

그리고 목적지까지 가는데 걸리는 시간이 바로 해의 값이고요

정리하면 다음과 같습니다.

IP 문제의 정수해의 Z값 =< IP 문제의 완화상태 실수해의 Z값 

그러면 상한이 90이라고 설정하고 다음할 작업은 분할을 실행할 변수를 선택하는 것입니다.

어떤 변수를 선택할지에 대해서 최적화된 방법이 있습니다만 여기서는 그냥 X1 , X2, X3... 이렇게 숫자 순서대로 합시다

그러면 X1을 어떻게하냐... 바로 1과 0을 대입합니다! 

그러면 위 이진 트리처럼 X1에 대해서 두개의 자식 노드가 생성됩니다.

다음 위 자식노드의 수식을 단체법을 이용하여 값을 구해줍니다. 

왼쪽 자식 노드

해 (1, 0, 0.4, 0)

값 90

오른쪽 자식 노드

해 ( 1, 0 , 0.2 , 0)

해 70

둘 다 정수해가 아니군요 따라서 하한을 설정할 수 없습니다.

일단 상한은 그대로 90입니다.

일단 둘다 분지를 해야하는데 왼쪽부터 분지해봅시다.

X2가 0과 1에 대해서 분지하면 다음과 같습니다.

이제 한눈에 봐도 쉽게 풀릴 정도로 수식이 나왔습니다.

일단 왼쪽 자식 노드를 살펴보면...

해는 (0, 0.8) 즉 (0,0,0,0.8)이며 값은 80입니다.

그런데 잘생각해보면 저런 문제는 그냥 눈으로 쓱 봐도 풀 수 있지 않나요?

딱봐도 저 문제의 정수해는 X3=1일 때 값이 50이라는 것을 알 수 있습니다.

원래 저 노드도 실수해가 나왔기 때문에 X3에 대해서 분지해야되지만 너무 많이 내려가네요 이쯤에서 그냥 눈으로 쓱 보고 풀 수 있으니 정수해 하나 구했다고 칩시다. 문제 잘못골랐네여

그래서 꼼수(?)를 합의봤다고 치고 정수해 (0, 0, 1, 0)을 얻었습니다. 이 해의 값은 50이죠

오른쪽도 마찬가지로 제약조건을 만족하는 정수해는 없으므로 (0, 1, 0, 0)을 얻었고 해의 값은 50입니다.

원래라면 왼쪽 오른쪽 정수해가 나올 때까지 분지해야합니다......

그러면 이제 정수해에 의해서 하한이 정해집니다.

상한 : 90

하한 : 50 (0,0,1,0), (0, 1, 0, 0)

다음은 X1=1일 때 X2에 대해서 분지해봅시다.

이번에도 두 자식노드 전부다 실수해기 때문에 분지가 되는군요......

그러면 오른쪽 노드만 분지하고 왼쪽은 암산으로 풉시다.

왼쪽 노드의 정수해를 구해보면 (1, 0, 0, 0)으로 값은 5가 됩니다. 이 값은 하한으로 설정해둔 50보다 작으므로 더 이상 분지할 필요가 없습니다.

반면 오른쪽 노드의 경우는 해가 (1, 1, 0, 0.2)가 나오며 이 값은 75가 됩니다.

따라서 상한과 하한 사이에 있으므로 이 노드를 한번 더 X3에 대해서 분지해 줍시다.

왼쪽은 X4가 0.2일 경우 해는 (1,1,0,0.2) 값은 75가 됩니다. 따라서 X4에 대해서 한번더 분지해줘야합니다........

오른쪽에서는  X4의 해가 0보다 같거나 커야하는데 위반하므로 해를 구할 수 없습니다.

따라서 오른쪽 노드는 더이상 분지하지 않습니다.

따라서 왼쪽 노드를 X4에 대해서 분지하면

위 그림과 같이 나오며 이 때 오른쪽 노드의 경우는 상항을 벗어났으므로 탈락

그리고 왼쪽 노드는 범위 안에 있으면서 하한값보다 높기 때문에 해 (1,1,0,0)이 최적해가 되며 그 값은 55입니다...

정리하면 

처음엔 정수해 문제를 실수해로 완화하고 단체법으로 풀기 여기서 정수해가 나오면 그걸로 사용합니다.

이때 처음 나온 실수해의 값 Z가 상한이되며 하한은 -oo입니다.

다음엔 특정 변수를 분지하기 

분지한 변수를 다시 단체법으로 풀고 정수해면 하한으로 설정

.... 이 작업의 반복이 바로 분지한계법입니다.

지금까지 분지한 그림

사실 분지한계법의 풀이는 이진 트리 형태를 띄고 있기 때문에 더 빨리 해를 찾을 수 있는 몇가지 수법이 존재합니다. 그 수법에 대해서는 언젠간 다른 포스터에서 다루기로 해봅시다.