일반화된 분지절단법이란 어떠한 정수계획법에도 쓸 수 있는 분지절단법을 말합니다.

저번에 썼던 포스트에서 정수계획법에 대한 간단한 설명과 기초 개념을 다뤘습니다.

그 후 정수계획법을 푸는 방법 중 하나인 분지절단법에 대해서 알아봤고 배낭문제에 적용하여 풀이를 해봤습니다.

그런데 생각해봅시다 저번에 풀었던 배낭문제는 결국 하냐 안하냐로 귀결되는 정수계획법의 한 분야인 0-1계획법 문제였습니다. 그러면 다른 정수계획법 문제에 분지절단법을 적용하려고 하면 어떻게 될까요??

저번에 다뤘던 배낭문제를 다시 꺼내봅시다.

여기서 분지절단법으로 풀때 X1을 분할 변수로 두고 0일 때와 1일 때로 두고 풀었습니다. 

이렇게 말이죠

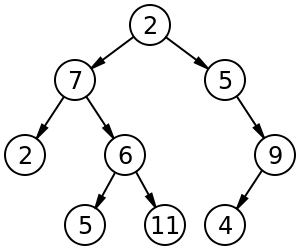
그리고 쭉쭉 분할해서 다음과 같은 그림을 얻었습니다.

그러면 만약 문제가 0-1계획법 문제가 아니라 그냥 정수계획법문제면 처음 시작할 때 어떻게 분할할지도 막막합니다.

그래서 이번 포스트에서는 다른 정수형문제도 막힘없이 풀기 위해서 일반화된 분지절단법을 알아보도록 합시다.

기본적인 초반의 흐름은 0-1계획법에서 했던 내용과 같습니다.

처음엔 하한을 무한으로 둔다... 상한은 문제를 단체법으로 푼 뒤 나오는 값을 사용한다. 이렇게 말이죠

근대 분지에서 약간 틀립니다.

한번 보시죠 내용은 (박순달 저)경영과학 제 3판 민영사에서 가져왔습니다.

단계 2. 분지

(1) 최적해에서 정수가 아닌 변수를 선택한다.

(2) 원문제에 다음 제약식을 각각 추가한 두 개의 새로운 문제를 문제목록에 등록한다.

단계 3  탐색

문제목록에서 문제 하나를 선택한다. 만일 비어 있으면 끝난다.

여기서 분지를 잘봅시다. 저기서 원문제에 관해 제약식을 추가하여 두 개의 새로운 문제를 등록하는 과정은 0-1계획법 분지계획법 풀이에서 보았던 트리가 생성되는 과정입니다.

또한 일반화된 분지절단법의 경우 저 제약식을 원래 문제에 집어 넣어 풀이를 하게 됩니다.

그런데 잘생각해봅시다.

0-1계획법에서는 처음에 x1에 0과 1을 넣어 분지했죠?? 이렇게 말이에요

그런데 잘생각해보면 이것 또한 제약식을 추가한 것과 같습니다. 

그 다음 저 제약식을 포함한 두개의 자식 노드로 나뉜거죠

아하 그럼 이제 눈에 보입니다.

바로 본질적으로 0-1계획법 풀이와 달라지지 않았다는 것이죠

전혀 새로운게 아니라 제약식에 부등호가 추가되었을 뿐입니다.

이제 어떻게 돌아가는지 대충 보이시죠?

그러면 문제 하나 풀어봅시다.

먼저 단체법으로 위 식을 풀어보면 

x1=13/4 , x2= 5/4 , x3=0, x4=0 그리고 최대값은 75/4입니다.

따라서 상한을 75/4=18.xxx로 설정할 수 있겠군요

그럼 먼저 간단하게 x1에 대해서 분지하도록 하고 기준을 3에 둡시다. 

일단 기준을 정했으면 제약식은 다음과 같습니다.

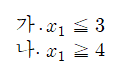
그 다음은?? 그냥 x1에 위 수식을 각각 대입하면됩니다

그러면 먼저 왼쪽 노드부터 생각해봅시다 

왼쪽 노드를 풀기 귀찮으니 단체법 계산기에 넣으면...

x1=3

x2=1.5

x3=0

x4=0.5    그리고 z값은 18이 되는군요

일단 이 해는 정수해가 아니므로 한번 더 분지시켜봅시다

왼쪽 자식노드를 x2에 대해서 기준값 1( 1은 0과 1 즉 2개를 내포하고 있죠?)에 관해서 분지하면

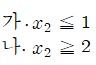
다음 왼쪽 노드를 계산기 넣고 돌려보면

x1=3

x2=1

x3=1

x4=1

Z=17 이 나옵니다

드디어 찾고 찾던 정수해 단! 하나가 나왔군요

일단 그러면 저 정수해를 기록해두고 하한을 17로 둡시다

다음 오른쪽도 돌려봐야죠?

오른쪽같은 경우는

x1=2.5

x2=2

x3=0

x4=1.5

z=16.5가 나옵니다

그런데 z값이 왼쪽에서 나온 하한인 17보다 작군요

그러면 더 이상 오른쪽 노드는 분지할 필요가 없습니다.

다음으로 다시 부모 노드로 돌아가서

이번엔 오른쪽 노드를 파해쳐봅시다

오른쪽노드의 해는 비가해 즉, 해를 구할 수 없다고 나옵니다.

그러면 현재까지 구한 정수해는 한개밖에 없죠??

그러면 이 문제의 해답은 

x1=3

x2=1

x3=1

x4=1 이며 Z=17 이 나옵니다

정리

이렇게 일반화된 분지한계법의 풀이는 살짝 더 복잡하지만 익숙해지면 정수계획은 문제없이 풀 수 있는 강력한 도구 중 하나입니다.

정수계획법은 특정 문제를 풀 때는 선형계획법보다 유용합니다.

집을 사냐 안사냐(0-1 계획법)

장난감을 몇개 살것인가(정수계획법)

그런데 정수계획법은 선형계획법에 속해 있는 한 분류이기 때문에 어떠한 대상에 대해서 수식으로 표현하려고하면 일단 선형계획법으로 표현하는게 훨씬 쉽습니다. 문제는 그러한 선형계획법으로 나타낸 수식을 어떻게 정수계획법으로 바꾸는지가 문제가 되죠

마치 초상화를 그릴때 선형계획법은 소묘와도 같으며 정수계획법은 그러한 소묘 위에 물감을 덧칠하는 수체화와 같습니다.

그러면 이번 이야기의 주제가 파악되셨나요?

바로 소묘 위에다 수체화를 덧칠하는 방법... 선형계획법을 정수계획법으로 바꾸는 방법에 대해서 알아봅시다.

먼저 몸풀이 예제 하나

O리온 사는 과자를 만드는 회사입니다.

이 회사에서 신제품 출시를 위해서 공장과 창고를 새로운 위치에 짓을려고 하려고합니다.

공장과 창고 후보지로는 부산과 강원도가 있습니다.

이때 조건이 있습니다.

1. 건설 예산은 100억원이 있습니다.

2. 창고는 최대 1개만 지을 수 있다고 합니다.

3. 한 지역에 공장을 하지 않는다면 그 지역에 창고는 필요 없다고 합니다.

이 때 이 문제를 어떻게 정수계획법으로 나타낼까요?

먼저 변수를 지정해 줍시다.

계획들 보기 순번대로 X1, X2, X3, X4로 배정해주면되는군요

다음은 목적함수를 구해야합니다.

기대 이익이 크면 클수록 좋으므로 다음 수식을 최대화하는게 목적이 되겠네요

최대화 : Z=90X1 + 50X2 + 60X3 + 40X4

다음으로는 제약 조건을 구해야합니다.

먼저 1. 에 대한 제약조건을 구해봅시다 이거는 건설 비용이 나와있으니 쉽게 구할 수 있습니다.

60X1 + 30X2 + 50X3 + 20X4 ≤ 100

양변을 10으로 나눠줍시다

6X1 + 3X2 + 5X3 + 2X4 ≤ 10

다음 조건 2. 를 생각해봅시다. 창고는 최대 1개만 지을 수 있으며 X3가 1이라는 뜻은 부산에 창고를 짓는다 X4가 1이라는 뜻은 강원도에 창고를 짓는다라는 뜻이므로 다음과 같이 조건을 나타낼 수 있습니다.

X3+X4 ≤ 1

마지막으로 3. 이 남았군요

잘 생각해봅시다 부산에 창고와 에 대해서 다음 표를 봅시다.

위 표를 보시면 X1 - X3할 때 항상 0보다 같거나 큰 값을 가진다는 걸 알 수 있습니다.

반대로 X3가 1이고 X1이 0인 경우만 음수 값을 가지네요

따라서 조건 3.을 표현하면 다음과 같습니다.

X1 - X3 ≥ 0 

X1 ≥ X3

이러한 방법을 강원도에도 적용시켜보면 

X2 ≥ X4

가 나옵니다.

따라서 위 수식을 정리하면 다음과 같습니다.

목적함수

최대화 : Z=90X1 + 50X2 + 60X3 + 40X4

제약조건

6X1 + 3X2 + 5X3 + 2X4 ≤ 10

X3+X4 ≤ 1

X1 ≥ X3

X2 ≥ X4

그리고 Xj 는 정수

(실수 값이 들어갈 수 있으니 정수 조건을 추가해줍니다)

자 이제 몸풀이가 끝났으니 본격적으로 시작해봅시다.

처음으로 알아볼 것은 제약조건에 OR이 들어간 경우입니다.

위 예제에서 제약 조건은 4개가 있었습니다.

제약조건

6X1 + 3X2 + 5X3 + 2X4 ≤ 10------1

X3+X4 ≤ 1--------------------------2

X1 ≥ X3 ----------------------------3

X2 ≥ X4 ----------------------------4

여기서 추가 조건으로 부산이나 강원도 둘 중 하나만 택해서 건설해야할 때 어떻게 수식을 수정해야할까요?

제약조건을 더 첨가해야할까요? 아니면 수식 수정을 해야할까요?

이런 문제를 Either-or constraints라 하며 이러한 제약은 생각보다 쉽게 수정이 가능합니다.

그 방법은 바로 추가 변수를 주는 방법입니다.

여기서 제약을 만족하려면 두 가지 새로운 변수를 도입해야하는데 먼저 무지막지하게 큰 수 M과 1과 0의 값만을 가지는 y라는 변수를 도입합니다.

그리고 다음과 같이 설정합니다.

My ≥ X3-X1 --------------------------------3

M(1-y) ≥ X4-X2 ----------------------------4

그러면 y가 만약 0이면 다음과 같이 되겠죠?

0 ≥ X3-X1 --------------------------------3

M ≥ X4-X2 --------------------------------4

여기서 M은 매우 큰 숫자이기 때문에 X4와 X2가 무슨 값이든 다 만족해버립니다.

즉 식 4의 경우는 필요없는 수식... 없는 수식과 마찬가지가 됩니다. 반대로 3번 수식은 처음 상태 그대로군요

이렇게 다시쓰면 다음과 같습니다.

목적함수

최대화 : Z=90X1 + 50X2 + 60X3 + 40X4

제약조건

6X1 + 3X2 + 5X3 + 2X4 ≤ 10

X3+X4 ≤ 1

My ≥ X3-X1

M(1-y) ≥ X4-X2

그리고 Xj 는 정수

y는 0 or 1

그런데 곰곰히 잘 생각해보면 이것을 일반화할 수 있지 않을까요??

그러니까 이러한 방법을 잘 이용하면 100개의 조건 중에서 10개나 20개 선택하는 것이 가능하지 않을까요?

그 방법은... 있습니다!

그러한 문제를 K out of N constraints라고 합니다.

조건이 10개중 3개를 선택한다면 다음과같이 나타낼 수 있습니다.

조건1

조건2

조건3

...

조건10

(Y1)조건1

(Y2)조건2

(Y3)조건3

...

(Y10)조건10

Yi는 0 or 1

이렇게 일반화를 하면 모양이 조금 안예뻐지긴 합니다. 그러면 다음으로 넘어가봅시다.

두번째로 알아볼 것은 초기 시작비용이 존재할 경우입니다.

만약 모 악덕 사체업자 너구리가 나오는 게임을 시작한다고 합시다

이 게임은 게임기가 필요합니다 그러면 게임을 하려면 게임기를 사야겠네요

즉 시도를 안하면 아무 비용도 없었던게 한다고 결정하면 비용이 생기게 됩니다.

요렇게 말이죠

수식으로 나타내면 다음과 같습니다.

그러면 이러한 문제를 어떻게 정수계획법으로 나타낼 수 있을까요?

이것도 간단하게 풀립니다.

바로 변수 y를 도입하는 것입니다.

그런데 y값은 여전히 조건문입니다.

이것을 어떻게 일반 제약 수식으로 바꿀 수 있을까요?

방법은 위에서 보던 M이라는 매우 큰 수를 도입하는것입니다.

이렇게되면 x가 0이면 y는 0 or 1의 값이 될 수 있으며 x가 1이면 y는 무조건 1이 되야합니다.

그런데 아직 문제가 남아있습니다. x가 0일 때 y는 1도 될 수 있기 때문입니다.

이러한 문제를 해결하기 위해선 상식문제 하나 풀어 봐야합니다.

과연 게임기를 안샀는데 게임을 살 필요가 있을까요 없을까요?

흠 수집마니아나 뭔가 꿍꿍이가 있는 사람이 아니면 게임기가 없는데 게임을 살 필요는 없겠죠?

그렇다면 게임기가 없을 때 게임이 있는 해는 고려하지 않아도 됩니다.

즉 다시 말하자면 x가 0일 때 y는 어떤 수가 되도 상관이 없다는 뜻이 됩니다.

이렇게 문제를 선형계획법으로 나타내고 그것을 정수계획법으로 바꾸는 방법도 알아봤습니다.

위의 방법을 잘 섞으면 못 나타낼 정수계획문제는 없다고 생각드네요!

정수계획법은 간단히 말하자면 선형계획법에서 정수해만을 인정하는 경우를 말합니다.

그래서 식은 선형계획법 식과 다름이 없습니다.

단지 제약이 해가 정수여야 한다는 것입니다.

그러면 이런걸 어디다 써먹을까요? 

바로 결정 문제에서 많이 쓰입니다. 서울에 집을 5채를 사겠다고 하지 4.3채를 사겠다고 하지 않잖아요

그런데 이러한 정수계획법에서 일부는 정수 해가 나오고 일부는 실수 해가 나올 수 있는데 이것을 혼합정수계획법(MIP)라고 합니다.

정수계획법에서는 이 정수라는 놈 때문에 선형계획법에서 편리하게 사용했던 단체법을 사용할 수가 없습니다.

그래서 정수계획법에서는 각 문제에 따라 알맞은 계산방법이나 근사해를 구하는 발견적 기법 즉, 휴라스틱을 사용합니다.

정수계획법 문제 예를 봅시다

많이들 들어본 배낭문제가 그 예중 하나입니다.

재미있게 보셨나요?

도둑은 결국 자전거만 끌고 집에 가는군요

영상에서는 욕심쟁이 알고리즘이 나왔지만 이거는 나중에 알아보도록 합시다.

이처럼 도둑도 포기하게 만든 배낭문제! 쉬워보이지만 깊게 파고들면 매우 복잡한 문제입니다.

예시를 들기 위해 위에서 나온 물품의 가치는 다음과 같다고 합시다.

가방에는 최대 20KG까지 들어갈 수 있으므로 위 문제를 수식으로 나타내면 다음과 같습니다.

여기서 X1이나 X2가 0.5와 같은 값을 가질 수 있을까요?

그러면 가장 가치있는 자전거를 0.5개.... 즉 반토막을 내서 가져가면 가치가 50만원일까요?

이렇게 가져가냐 안가져가냐를 따지는 문제... 더 포괄해서 하는가 않하는가를 따지는 문제를 0-1계획법이라고 합니다. 

그러면 정수계획법의 대략적인 문제의 형태가 보이기 시작합니다.

그러면 이제 이 문제를 해결할 수 있는 해법에 대해 토의하기 

이러한 정수계획법의 휴라스틱 해법으로는 두가지가 있습니다.

절단평면법

분지한계법

이 두가지 방법을 모두 설명하려고하면 분량이 매우 많기 때문에 절단평면법은 다른 포스터에서 다뤄보기로 하고 이 포스터에서는 분지한계법을 알아보도록 합시다.

그러면 차근차근 해법을 살펴보도록 합시다.

 *분지한계법(Branch-and-bound technique)

이 방법은 모든 가능해를 계산하는 열거식의 일종입니다.

모든 해를 계산하는게 바보같고 택틱컬하지 않다고요?

아뇨 모든 가능한 방법을 검토해보는건 100% 가장 확실한 방법입니다.

단지 시간이 조금 오래 걸릴뿐이죠..

분지한계법은 쪼개서 정복하는 알고리즘입니다. 큰 해영역에서 진짜 이 영역은 아무리 봐도 아니다싶은 부분은 잘라내고 남은 영역에서 탐색하고 또 잘라내고 탐색하는것을 반복하는거죠.

따라서 분지한계법은 이진트리의 형태를 띄고 있습니다.

대강 이런 느낌...

그리고 또 중요한건 탐색하면서 해의 상한과 하한을 정한다는 특이한 점이 있습니다.

이거는 지금 설명하면 이해가 잘안될 수 있으니 예를 보고 갑니다.

실제 알고리즘은 3단계로 간단한 편입니다. 

분지 -> 한계설정 -> 살펴보기 -> 분지 -> 한계설정 -> 살펴보기 .... 

위 배낭문제를 예로 들어봅시다.

먼저 위 식에서 수정해야할 점은 해가 정수라는 조건을 없애는 것입니다.

더 정확히는 해가 0~1까지로 제한합니다.

이렇게 해의 조건을 완화하는 것을 Relaxation이라 하는데 조건을 완화함으로 더 쉽게 문제를 풀 수 있습니다.

위 수식을 제약조건을 완화하여 다시쓰면 다음과 같습니다.

다음 해야할 것은 위 수식을 일단 단체법으로 풀어봐야합니다.

풀면 최적해는 (0, 1, 0, 0.4)로 나오며 값은 90이 되는데 이 90이라는 값이 바로 앞으로 풀면서 나올 모든 값들의 상한이 됩니다.

왜냐하면 정수해는 실수해보다 값이 반드시 같거나 작기 때문입니다.

비유를 하자면... 만약 자동차와 비행기가 같은 목적지로 간다고 생각해봅시다. 비행기는 밑에 건물이 있던 없던 쌩하고 목표까지 날아갈 수 있는데 자동차는 도로나 여러 신호를 봐가면서 가야하기 떄문에 훨씬 시간이 오래 걸립니다.

이때 공중을 아무 제약조건도 없는 상황 그리고 도로나 여러 신호상황을 정수 제약조건으로 봐도 무방합니다.

그리고 목적지까지 가는데 걸리는 시간이 바로 해의 값이고요

정리하면 다음과 같습니다.

IP 문제의 정수해의 Z값 =< IP 문제의 완화상태 실수해의 Z값 

그러면 상한이 90이라고 설정하고 다음할 작업은 분할을 실행할 변수를 선택하는 것입니다.

어떤 변수를 선택할지에 대해서 최적화된 방법이 있습니다만 여기서는 그냥 X1 , X2, X3... 이렇게 숫자 순서대로 합시다

그러면 X1을 어떻게하냐... 바로 1과 0을 대입합니다! 

그러면 위 이진 트리처럼 X1에 대해서 두개의 자식 노드가 생성됩니다.

다음 위 자식노드의 수식을 단체법을 이용하여 값을 구해줍니다. 

왼쪽 자식 노드

해 (1, 0, 0.4, 0)

값 90

오른쪽 자식 노드

해 ( 1, 0 , 0.2 , 0)

해 70

둘 다 정수해가 아니군요 따라서 하한을 설정할 수 없습니다.

일단 상한은 그대로 90입니다.

일단 둘다 분지를 해야하는데 왼쪽부터 분지해봅시다.

X2가 0과 1에 대해서 분지하면 다음과 같습니다.

이제 한눈에 봐도 쉽게 풀릴 정도로 수식이 나왔습니다.

일단 왼쪽 자식 노드를 살펴보면...

해는 (0, 0.8) 즉 (0,0,0,0.8)이며 값은 80입니다.

그런데 잘생각해보면 저런 문제는 그냥 눈으로 쓱 봐도 풀 수 있지 않나요?

딱봐도 저 문제의 정수해는 X3=1일 때 값이 50이라는 것을 알 수 있습니다.

원래 저 노드도 실수해가 나왔기 때문에 X3에 대해서 분지해야되지만 너무 많이 내려가네요 이쯤에서 그냥 눈으로 쓱 보고 풀 수 있으니 정수해 하나 구했다고 칩시다. 문제 잘못골랐네여

그래서 꼼수(?)를 합의봤다고 치고 정수해 (0, 0, 1, 0)을 얻었습니다. 이 해의 값은 50이죠

오른쪽도 마찬가지로 제약조건을 만족하는 정수해는 없으므로 (0, 1, 0, 0)을 얻었고 해의 값은 50입니다.

원래라면 왼쪽 오른쪽 정수해가 나올 때까지 분지해야합니다......

그러면 이제 정수해에 의해서 하한이 정해집니다.

상한 : 90

하한 : 50 (0,0,1,0), (0, 1, 0, 0)

다음은 X1=1일 때 X2에 대해서 분지해봅시다.

이번에도 두 자식노드 전부다 실수해기 때문에 분지가 되는군요......

그러면 오른쪽 노드만 분지하고 왼쪽은 암산으로 풉시다.

왼쪽 노드의 정수해를 구해보면 (1, 0, 0, 0)으로 값은 5가 됩니다. 이 값은 하한으로 설정해둔 50보다 작으므로 더 이상 분지할 필요가 없습니다.

반면 오른쪽 노드의 경우는 해가 (1, 1, 0, 0.2)가 나오며 이 값은 75가 됩니다.

따라서 상한과 하한 사이에 있으므로 이 노드를 한번 더 X3에 대해서 분지해 줍시다.

왼쪽은 X4가 0.2일 경우 해는 (1,1,0,0.2) 값은 75가 됩니다. 따라서 X4에 대해서 한번더 분지해줘야합니다........

오른쪽에서는  X4의 해가 0보다 같거나 커야하는데 위반하므로 해를 구할 수 없습니다.

따라서 오른쪽 노드는 더이상 분지하지 않습니다.

따라서 왼쪽 노드를 X4에 대해서 분지하면

위 그림과 같이 나오며 이 때 오른쪽 노드의 경우는 상항을 벗어났으므로 탈락

그리고 왼쪽 노드는 범위 안에 있으면서 하한값보다 높기 때문에 해 (1,1,0,0)이 최적해가 되며 그 값은 55입니다...

정리하면 

처음엔 정수해 문제를 실수해로 완화하고 단체법으로 풀기 여기서 정수해가 나오면 그걸로 사용합니다.

이때 처음 나온 실수해의 값 Z가 상한이되며 하한은 -oo입니다.

다음엔 특정 변수를 분지하기 

분지한 변수를 다시 단체법으로 풀고 정수해면 하한으로 설정

.... 이 작업의 반복이 바로 분지한계법입니다.

지금까지 분지한 그림

사실 분지한계법의 풀이는 이진 트리 형태를 띄고 있기 때문에 더 빨리 해를 찾을 수 있는 몇가지 수법이 존재합니다. 그 수법에 대해서는 언젠간 다른 포스터에서 다루기로 해봅시다.